Главная /
Ассемблер /
Для чайников /
Системы счисления /
Двоичная система счисления
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа.
А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число
оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два
состояния – вЫключено и включено (или нет напряжения – есть напряжение).
Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения
на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод
может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо,
потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете
почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например,
шины данных или
шины адреса.
И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов
на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе,
которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего
двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2.
Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд).
Четыре бита – это полубайт (или тетрада), 8 бит – байт,
16 бит – слово, 32 бита – двойное слово. Запомните эти термины,
потому что в программировании они используются очень часто. Возможно, вам уже приходилось
слышать фразы типа слово данных или байт данных. Теперь,
я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый
младший бит (нулевой бит) является крайним справа. Слева находится
старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й.
В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер)
будете знать, что это двоичное число. Например,
101 – это десятичное число
101b – это двоичное число, которое эквивалентно десятичному числу 5.
А теперь попробуем понять, как формируется
двоичное число.
Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного
числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду.
Тетрада (или полубайт) имеет 4 бита.
| Двоичное |
Десятичное |
Пояснения |
| 0000 |
0 |
- |
| 0001 |
1 |
В младший бит устанавливается 1. |
| 0010 |
2 |
В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 |
3 |
В младший бит устанавливается 1. |
| 0100 |
4 |
В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются. |
| 0101 |
5 |
В младший бит устанавливается 1. |
| 0110 |
6 |
Продолжаем в том же духе... |
| 0111 |
7 |
... |
| 1000 |
8 |
... |
| 1001 |
9 |
... |
| 1010 |
10 |
... |
| 1011 |
11 |
... |
| 1100 |
12 |
... |
| 1101 |
13 |
... |
| 1110 |
14 |
... |
| 1111 |
15 |
... |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями
и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица,
то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и
в десятичной системе:
0…9
10 – очищаем младший разряд, а в старший добавляем 1
Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать
16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее.
На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
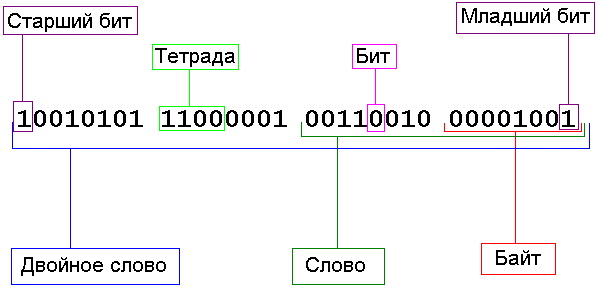
Рис. 2.2. Двоичное число.